Time Complexity
Time complexity is the computational complexity that describes the amount of time it takes to run a program. The time complexity is calculated by counting the number of elementary operations performed by a program or algorithm. Since and algorithm's running time could vary greatly from the inputs given to it. When calculating the time complexity of the algorithm, we use the worst case time complexity for any given input to the algorithm.
What is Big O notation?
Big O notation is a mathematical representation that describes the limiting behavior of an algorithm as the input size reaches infinity. It is used to classify algorithms by their respective run time which in turn helps software developers improve the performance of their algorithms. Some examples of big O notations are: O(1), O(n), O(n^2), O(log n).
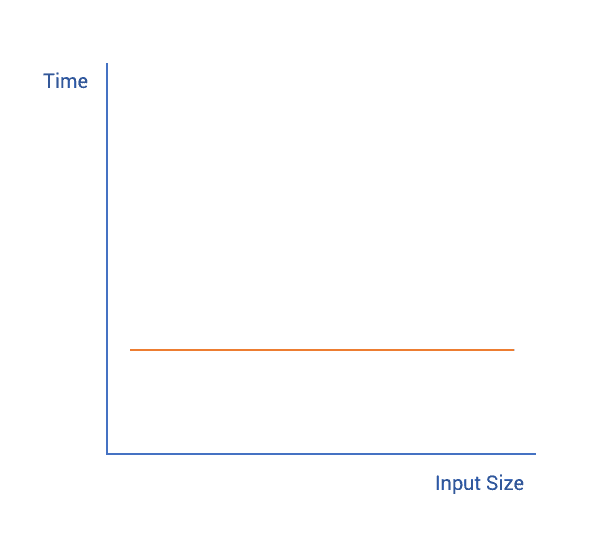
Constant Time
Constant time is when an algorithm's time complexity doesn't depend on the size of the input. For example:
// Getting median value of a sorted array.
function getMedian(sortedArr) {
const arrLen = sortedArr.length // O(1)
const midIndex = Math.floor(arrLen / 2) // O(1)
return sortedArr[midIndex] // O(1)
}
// Time complexity
// T(n) = O(1) + O(1) + O(1) = O(1)In the example we can see that the length of the sortedArr will not affect the time it would take to get its median. Therefore, we can consider this function's time complexity to be constant. Something to keep in mind is that, constant time refers to a time complexity's upper bound. For example, an algorithm could take different times to perform a task but would never go over some upper limit. This upper limit is how we determine that the algorithm has a constant time complexity. The notation used for constant time is O(1).
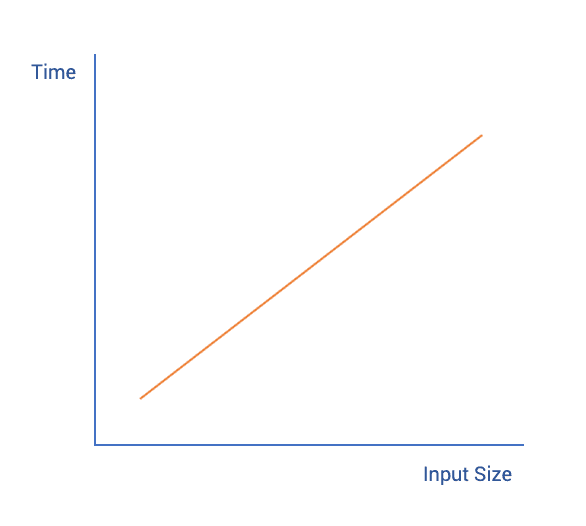
Linear Time
Linear time is when an algorithm takes O(n) time complexity. This means that the time is directly proportional to the algorithms input. For example:
// Print array values
function printValues(arr) {
for (let i = 0; i < arr.length; i++) {
console.log(arr[i]) // O(n)
}
}
// Time complexity
// T(n) = O(n)For linear time is the best possible time complexity and thus most algorithms try to achieve linear time complexity.
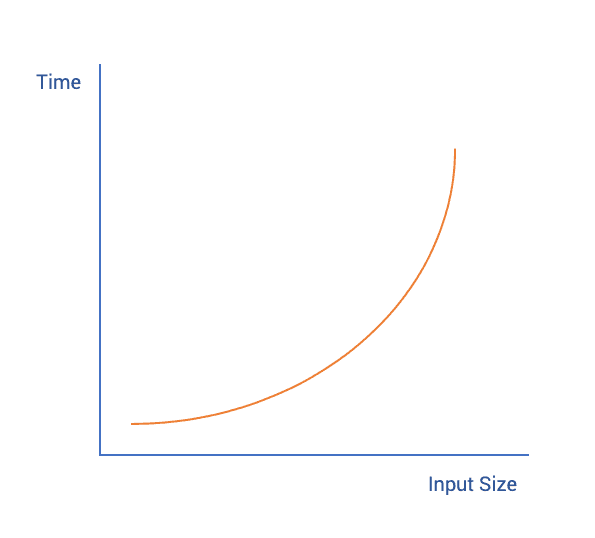
Quadratic Time
Quadratic time complexity is written as O(n^2) which means that it will scale in proportion to the square of the input.
// Find the common values between two arrays
function findCommon(arr1, arr2) {
const common = []
for (let i = 0; i < arr1.length; i++) {
for (let j = 0; j < arr2.length; j++) {
if (arr1[i] === arr2[i]) common.push(arr1[i]) // O(n * n) = O(n^2)
}
}
return common
}
// Time complexity
// T(n) = O(n * n) = O(n^2)Comparison based sorting algorithms are quadratic such as insertion sort, quick sort, selection sort, bubble sort, cycle sort, strand sort, library sort, and gnome sort.
Table of common time complexities
| Big O | Time Complexity T(n) |
|---|---|
| O(1) | Constant |
| O(log n) | Logarithmic |
| O(n) | Linear |
| O(n * log n) | Log Linear |
| O(n*) | Quadratic |